Параллельные миры.
Философское эссе-шутка, но …
Как мы знаем, для того, чтобы получить сечение n–мерного пространства, необходимо взять (n-1)-мерную пилу, или топор, и сделать это сечение.
Это, конечно, шутка, но, как мы тоже знаем: в каждой шутке есть только доля шутки, все остальное – правда и, в данном случае, это шуткой является только в плане пилы и топора.
Рассмотрим некоторые сечения:
Точка – есть сечение прямой,
Прямая – есть сечение плоскости,
Плоскость – есть сечение 3-мерного пространства и, так далее.
Поскольку мы живем в 4-мерном пространстве-времени, по крайней мере, это утверждается нашей наукой, то, для того, чтобы провести его сечение, нам необходимо взять 3-мерную пилу – событие 3-мерного пространства, и сделать это сечение.
Таким образом, можно обозначить множество событий сечения 4-мерного пространства-времени как некое плоское множество событий.
Обозначим это плоское множество как G.
Если мы берем пространство в «чистом» виде – положим отсутствие каких-либо взаимодействий, то сечение 4-мерного пространства-времени будет являть собой плоское множество несвязанных объектов.
Таким образом, свободное перемещение независимой системы отсчета в 4-мерном пространстве-времени от точки «А» до точки «В» можно представить единичными множествами GA и GB, связанными между собой определенным соответствием.
Если же перемещение системы отсчета происходит в условиях множественного взаимодействия с другими такими же системами, то множество GB уже представляет собой не единичное множество, а n–мерное множество. Каждый член этого множества определяется вероятностью своего существования, определяемой полем причин, в котором находится система отсчета в начальный момент своего перемещения.
Таким образом, будущее любого события из пространства-времени можно представить в виде n–мерного плоского множества, где каждый его член определяется полем причин, в котором находится событие.
Схематически это можно представить себе следующим образом:
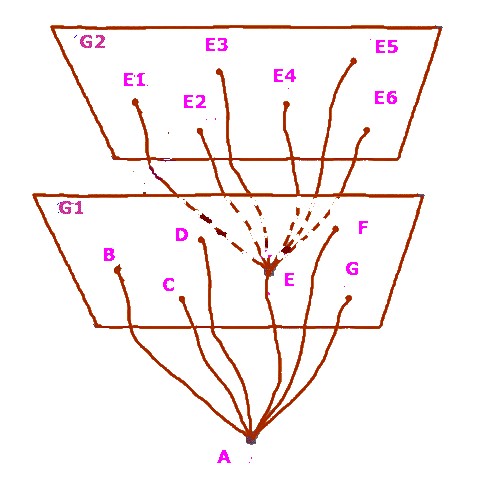
Исходя из вышеизложенного, будущее любого объекта-события из пространства-времени можно представить n–мерным множеством каждый член, которого определяется собственной плотностью вероятности в поле причин, определяющего существование этого события.
Таким образом, мы можем говорить, при исследовании будущего событий, о той или иной вероятности его проявления как его будущего. Следовательно, будущее любого события расслаивается на множество возможных пространств-событий в в континууме его возможного проявления.
Теперь, на основе предложенного вам представления, можно, пожалуй, утверждать, что будущее любого события в цепи проявлений этого события как творение сущего, поскольку каждое такие событие есть новое состояние сущего, расслаивается на множество возможных событий. Вот это множество возможных событий и представляет собой множество параллельных миров, существующих в разных причинно-следственных потоках.
Можно попробовать, с помощью реального моделирования причинных полей, осуществить переход из одного причинно-следственного потока в другой. Это будет равносильно переходу из одной вселенной в другую.
И, пожалуй, можно найти такой причинно-следственный поток, ведь вероятность его существования не нулевая, в котором я встречаюсь сам с собой (точка «С» на рисунке ниже).
Таким образом, мировую линию любого события из пространства его проявления, как его будущее и как акт непрерывного его творения, можно представить в виде ветвящегося дерева из всех возможных его состояний в континууме его проявления, определяемого полем причин, в котором оно находится.
Из изложенного представления также следует, возможность предсказания его будущего в поле существующих причин. И именно поэтому, на мой взгляд, мы и имеем факты прорицания будущего не только людьми, но и любыми существами, являющими собой акты непрерывного миротворения.
И здесь также хотелось бы отметить, как факт, вытекающий и предложенного представления, что, изменяя поле причин, своей возможной реализации, например, его деградируя, мы деградируем и множество возможных своих состояний, превращая его в нулевое множество.
Параллельные миры. Выпуск 359 (02.11.2017). Самые шокирующие гипотезы.